Unit-2:Limit and Continuity

 

Provide by:-bca-wala.blogspot.com

 Ankit Rajbansi😍

Unit-2:Limit and Continuity

Properties of Limit

There are three basic types of discontinuities:

1. Removable (point) discontinuity – the graph has a hole at a single x-value. Imagine you’re walking down the road, and someone has removed a manhole cover (Careful! Don’t fall in!). This function will satisfy condition #2 (limit exists) but fail condition #3 (limit does not equal function value).
2. Infinite discontinuity – the function goes toward positive or negative infinity. Imagine a road getting closer and closer to a river with no bridge to the other side
3. Jump discontinuity – the graph jumps from one place to another. Imagine a superhero going for a walk: he reaches a dead end and, because he can, flies to another road.

Intermediate Value Theorem Statement

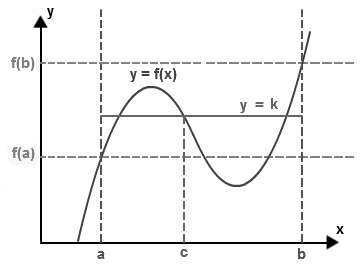
Intermediate value theorem states that if “f” be a continuous function over a closed interval [a, b] with its domain having values f(a) and f(b) at the endpoints of the interval, then the function takes any value between the values f(a) and f(b) at a point inside the interval. This theorem is explained in two different ways:

Statement 1:

If k is a value between f(a) and f(b), i.e.

either f(a) < k < f(b) or f(a) > k > f(b)

then there exists at least a number c within a to b i.e. c ∈ (a, b) in such a way that f(c) = k

Statement 2:

The set of images of function in interval [a, b], containing [f(a), f(b)] or [f(b), f(a)], i.e.

either f([a, b]) ⊇ [f(a), f(b)] or f([a, b]) ⊇ [f(b), f(a)]

Theorem Explanation:

The statement of intermediate value theorem seems to be complicated. But it can be understood in simpler words. Let us consider the above diagram, there is a continuous function f with endpoints a and b, then the height of the point “a” and “b” would be “f(a)” and “f(b)”.

If we pick a height k between these heights f(a) and f(b), then according to this theorem, this line must intersect the function f at some point (say c), and this point must lie between a and b.

An intermediate value theorem, if c = 0, then it is referred to as Bolzano’s theorem.

Intermediate Theorem Proof

We are going to prove the first case of the first statement of the intermediate value theorem since the proof of the second one is similar.

We will prove this theorem by the use of completeness property of real numbers.The proof of “f(a) < k < f(b)” is given below:

Let us assume that A is the set of all the values of x in the interval [a, b], in such a way that f(x) ≤ k.

Here A is supposed to be a non-empty set as it has an element “a” and also A is bounded above by the value “b”.

Thus, by completeness property, we have that, “c” be the lowest value which is greater than or equal to each element of A. Hence, we can say that f(c) = k.

Given that f is continuous. Then let us consider a ε > 0, there exists “a δ > 0” such that

| f(x) – f(c) | < ε for every | x – c | < δ. This gives us

f(x) – ε < f(c) < f(x) + ε

For each x lying within c – δ and c + δ. So, we have values of x lying between c and c -δ, contained in A, such that :

f(c) < (f(x) + ε) ≤ (k + ε) ——– (1)

Similarly, values of x between c and c + δ that are not contained in A, such that

f(c) > (f(x) – ε) > (k − ε) ——–(2)

Combining both the inequality relations, obtain

k – ε < f(c) < k + ε

For every ε > 0

Hence, the theorem is proved.

For more bca notes than visit us👈👈